บทนำ

สิ่งที่ปรากฏตามธรรมชาติมิได้มีแต่รูปร่างง่ายๆ เท่านั้น บางอย่างมีรูปร่าง ที่มีแบบแผนทางคณิตศาสตร์ที่ยุ่งยากขึ้นไปอีก ตัวอย่างที่น่าสนใจของธรรมชาติ ที่เป็นไปตามกฎเกณฑ์ของคณิตศาสตร์ชั้นสูง ได้แก่ เส้นโค้งก้นหอย ซึ่งมี คุณสมบัติว่า ถ้าลากเส้นตรงจากจุดหลายของเกลียวข้างในสุดไปตัดกับเส้นโค้งแล้ว มุมที่เกิดจากเส้นตรงนั้นกับเส้นสัมผัสกับเส้นโค้ง ณ จุดตัดจะเท่ากันเสมอ ดังรูป มุม A = มุม B = มุม C

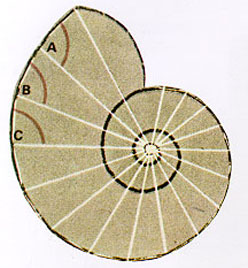
เส้นโคังที่มีลักษณะเป็นก้นหอยจะพบได้ในหอยบางชนิด เช่น หอยทาก นอกจากนี้ยังมีความโค้งของงาช้าง ความโค้งของเกสรดอกทานตะวัน ตามสับปะรด และ ตาลูกสน ก็มีลักษณะคล้ายส่วนของเส้นโค้งก้นหอยด้วย

ยังมีเรื่องที่น่าสนใจในธรรมชาติที่เกี่ยวข้องกับคณิตศาสตร์อีก จากการศึกษาเส้นโค้งของตาลูกสน ตาสับปะรด และ เกสรดอกทานตะวัน จะเห็นว่า เส้นโค้งที่หมุนตามเข็มนาฬิกาของตาลูกสนมีจำนวน ๕ เส้น และ หมุนทวนเข็มนาฬิกามีจำนวน ๓ เส้น หรือ อาจกล่าวได้ว่า จำนวนเส้นโค้งสองแบบ มีอัตราส่วนเป็น ๕ ต่อ ๘ สำหรับตาสับปะรด เส้นโค้งตามาเข็มนาฬิกา และ ทวนเข็มนาฬิกา มีอัตราส่วนเป็น ๘ ต่อ ๑๓ เส้นโค้งที่เกิดจากเกสรดอกทานตะวันตามเข็มนาฬิกา และ ทวนเข็มนาฬิกามีอัตราส่วนเป็น ๒๑ ต่อ ๓๔

ปรากฏการณ์นี้เป็นไปตามกฎเกณฑ์ของอันดับชนิดหนึ่งที่มีชื่อว่า อันดับฟิโบนักชี ที่นักคณิตศาสตร์ชาวอิตาลี แห่งเมืองปีซา (Pisa) ชื่อเลโอนาร์ โด ฟิโบนักชี (Leonardo Fibonacci ค.ศ. ๑๑๗๐-๑๒๔๐) เป็นผู้ค้นพบ

อันดับนั้นมีลักษณะดังนี้ ๑, ๑, ๒, ๓, ๕, ๘, ๑๓, ๒๑, ๓๔, ๕๕,...
พจน์ที่หนึ่ง และ พจน์ที่สองของอันดับเป็น ๑ พจน์ต่อๆ ไปได้จากผลบวกของสองพจน์ที่อยู่ติดกันจะเห็นได้ว่า อัตราส่วนของเส้นโค้งของตาลูกสน ซึ่งเท่ากับ ๕ กับ ๘ อัตราส่วนของเส้นโค้งของตาสับปะรดที่เท่ากับ ๘ ต่อ ๑๓ และ อัตราส่วนของเส้นโค้งของเกสรดอกทานตะวันที่เท่ากับ ๒๑ ต่อ ๓๔ นั้น ตัวเลขที่อยู่ในอัตราส่วนเหล่านี้เป็นพจน์สองพจน์ที่อยู่ติดกันในอันดับนี้

ตัวอย่างจากธรรมชาติที่เป็นไปตามอันดับฟิโบนักชี ได้แก่ การกำเนิดของผึ้ง

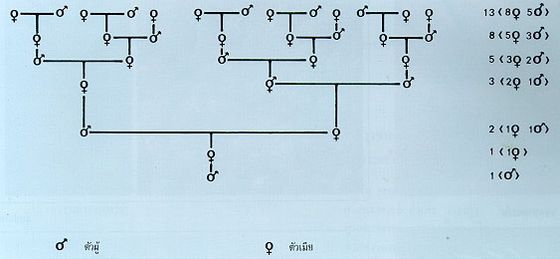
ความเจริญของพืช เช่น สาหร่าย ก็จะมีรูปแบบเช่นนี้

อันดับฟิโบนักชีนอกจากจะเกี่ยวข้องในวิชาชีววิทยาแล้ว ยังมีอิทธิพลในด้านศิลปะ และ สถาปัตยกรรม นั่นคือ อัตราส่วนระหว่างพจน์ที่ และ พจน์ที่หกของอันดับ ซึ่งได้แก่ ๕ ต่อ ๘ หรือ ๑ ต่อ ๑.๖ อัตราส่วนนี้มีชื่อว่า อัตราส่วนโกเดน (Golden Ratio) หรือ ส่วนแบ่งโกลเดน (Golden Section) เป็นที่ยอมรับกันว่า รูปสี่เหลี่ยมผืนผ้าที่อัตราส่วนของด้านกว้าง และ ด้านยาวเป็น ๑ ต่อ ๑.๖ จะเป็นรูปที่มีสัดส่วนสวยงามที่สุด และ มีชื่อว่าสี่เหลี่ยมผืนผ้าโกลเดน (Golden Rectangle) ถ้าจะสร้างรูปสี่เหลี่ยมผืนผ้าโกลเดนโดยใช้เรขาคณิตจะทำได้ดังนี้ เริ่มต้นสร้างรูปสี่เหลี่ยมจัตุรัส ABCD แล้ว แบ่งออกเป็นสองส่วนเท่า ๆ กันด้วย เส้นประ EF ใช้ F เป็นจุดศูนย์กลาง รัศมียาวเท่าเส้นทะแยงมุม FC เขียนส่วนโค้ง CG ไปตัดด้าน AD ต่อออกไปที่ G จะได้ AG เป็นด้านยาวของสี่เหลี่ยมผืนผ้า ลาก GH ตั้งฉากกับ AG พบ BC ต่อออกไปที่ H จะได้ GH เป็นด้านกว้างของสี่เหลี่ยมผืนผ้า รูป ABHG เป็นรูปสี่เหลี่ยมผืนผ้าโกลเดน และ รูป CDGH ก็เป็นรูปสี่เหลี่ยมผืนผ้าโกเดน

ตัวอย่างของอัตราส่วนโกลเดนที่ปรากฎในสถาปัตยกรรม เช่น